仿射变换

图像的仿射变换是将图像的二维坐标从一个直角坐标系中变换到另外一个直角坐标系中的二维坐标的过程。图像的仿射变换是一种线性的变换，可以表示为矩阵相乘。仿射变换主要用来实现图像的缩放，平移，旋转以及翻转，剪切等几何操作。

假设在空间中图像的原始坐标为（x,y）经过仿射变换后的目标坐标为（x’,y’），常见的变换形式有以下几种：

缩放：

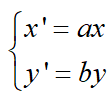
平移：

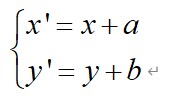
翻转：

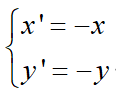
旋转：

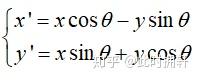
所有的仿射变换都是一种线性的变换，都可以使用矩阵的形式来表达，对于图像的平移变换都可以使用下面矩阵乘法的形式表示：

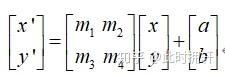
在opencv中构造变换矩阵通常是构造成2x3的矩阵即：

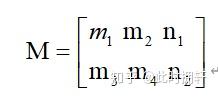
对于平移操作构造的矩阵为：

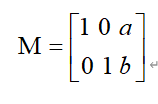
对于缩放而言，水平缩放因子为a,竖直缩放因子为b,则M矩阵为：

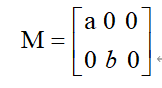
对于旋转而言，旋转角为θ时，则M矩阵为：

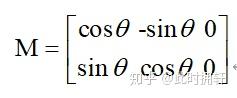
在看代码之前首先看一下warpAffine函数，函数原型如下：

Cv::warpAffine(InputArray src,

OutputArray dst,

InputArray M,

Size dsize,

int flas =INTER_LINEAR,

int borderMode = BORDER_CONSTANT,

const Scalar& borderValue = Scalar()

);

其使用的公式是

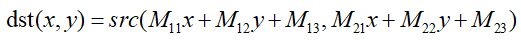
其参数：

src : 输入图像

dst : 输出图像，大小类型和src一样

M ：2x3大小的变换矩阵

dsize : 输出图像的大小

flags : 插值算法标志，如果结合使用WARO_INVERSE_MAP，表示仿射变换逆运算即（dst->src）

borderMode: 边界插值类型

borderValue :表示边界插值数据。

示例代码如下：

#include <iostream>
#include <string>
#include <cmath>
#include <opencv2/opencv.hpp>
using std::sin;
using std::cos;
//使用CommandLineParser对输入的参数进行分析，获取输入的图片路径
std::string GetFileName(int argc,char* argv[])
{
    /*
    argc : the size of argv[]
    argv : the parameters of comdline
    */
    const char* key = {
    "{help h usage? || usage information}"
    "{@picture || input picture}"
    };
     cv::CommandLineParser parser(argc,argv,key);
    if (parser.has("help"))
    {
        parser.printMessage();
        exit(0);
    }
    //如果没有输入图片路径
    if (!parser.check())
    {
        parser.printErrors();
        exit(-1);
    }
    std::string fileName = parser.get<std::string>(0);
    return fileName;
}
cv::Mat getRotationMatrix(cv::Point center,double angle,double scale)
{
    /*
    center : the center point of transform
    angle  : the angle of rotation
    scake  : the scale of zoom
    */
    angle *= CV_PI / 180 ;//angle to rad
    double alpha = scale * cos(angle);
    double beta =  scale * sin(angle);

    cv::Mat Matrix(2,3,CV_64F);
    double *m = (double*)Matrix.data;
    m[0] = alpha;
    m[1] = beta;
    m[2] = (1 - alpha) * center.x - beta * center.y;
    m[3] = -beta;
    m[4] = alpha;
    m[5] = beta * center.x + (1-alpha) * center.y;
    return Matrix;
}
int main(int argc,char* argv[])
{
      std::string ImageFilePath = GetFileName(argc,argv);
    cv::Mat srcImage = cv::imread(ImageFilePath);
    if (srcImage.empty())
    {
        std::cerr << "fail to load image" <<std::endl;
        exit(-1);
    }

    cv::Point center(srcImage.rows/2,srcImage.cols / 2);
    cv::Mat Mask = getRotationMatrix(center,60,1.0);
    cv::Mat dstImage(srcImage.size() ,srcImage.type());
    cv::warpAffine(srcImage,dstImage,Mask,dstImage.size());

    cv::imshow("srcImage",srcImage);
    cv::imshow("dst",dstImage);
    cv::waitKey(0);
    cv::destroyAllWindows();
    return 0;
}

输入图像为：

输出图像为：

赏

谢谢你请我吃糖果